Harmonic chains with hard wall constraints in classical and quantum mechanics

Ich heiße Dominik Hahn und war ab meinem dritten Semester (WS 2016/17) bis zu meinem Master-Abschluss 2020 Mitglied im Forschungsstudiengang. Im Augenblick bin ich Doktorand am Max-Planck-Institut für die Physik komplexer Systeme in Dresden.

Meine Masterarbeit habe ich am Lehrstuhl von Prof. Klaus Richter in einer Kollaboration mit Prof. Shivaji Sondhi von der Princeton University geschrieben, in dessen Rahmen ich drei Monate in Princeton als „Visiting Research Student“ gearbeitet habe.

In meiner Arbeit habe ich mich mit einem Phänomen befasst, das uns überall im Alltag begegnet:
Warum tendieren Systeme dazu, sich in ein thermisches Gleichgewicht zu bewegen? Ein Beispiel hierfür ist der Kaffee am Morgen, der sich nach einiger Zeit auf Raumtemperatur abkühlt. Es ist auch sehr spannend zu erforschen, ob sich dieser Vorgang unter bestimmten Bedingungen vermeiden lässt, dies kann dann in der Zukunft vielleicht zum Speichern von Daten in einem Quantencomputer genutzt werden.

Unser Modell. Die Teilchen sind in einer Box eingesperrt. Benachbarte Teilchen sind durch eine Feder miteinander verbunden.

Um das zu verstehen, haben wir ein einfaches Modell entwickelt, das aus Teilchen in einer Kiste besteht, die durch Federn verbunden sind. Wir haben dann unter anderem untersucht, wie lange es dauert, dass ein schnelles Teilchen seine ganze Energie an seine Nachbarn abgibt und so in ein Gleichgewicht gelangt.

Es stellt sich heraus, dass Chaos eine große Rolle spielt. Ein System ist chaotisch, wenn es sehr empfindlich auf kleine Störungen reagiert. Das bekannteste Beispiel ist der „Butterfly-Effekt“, nämlich dass ein Flügelschlag eines Schmetterlings in Südamerika das Wetter in Europa beeinflussen kann. Wenn das Modell für fast alle Anfangsbedingungen chaotisch ist, gelangt es dann auch nach einiger Zeit zu einem Gleichgewicht.

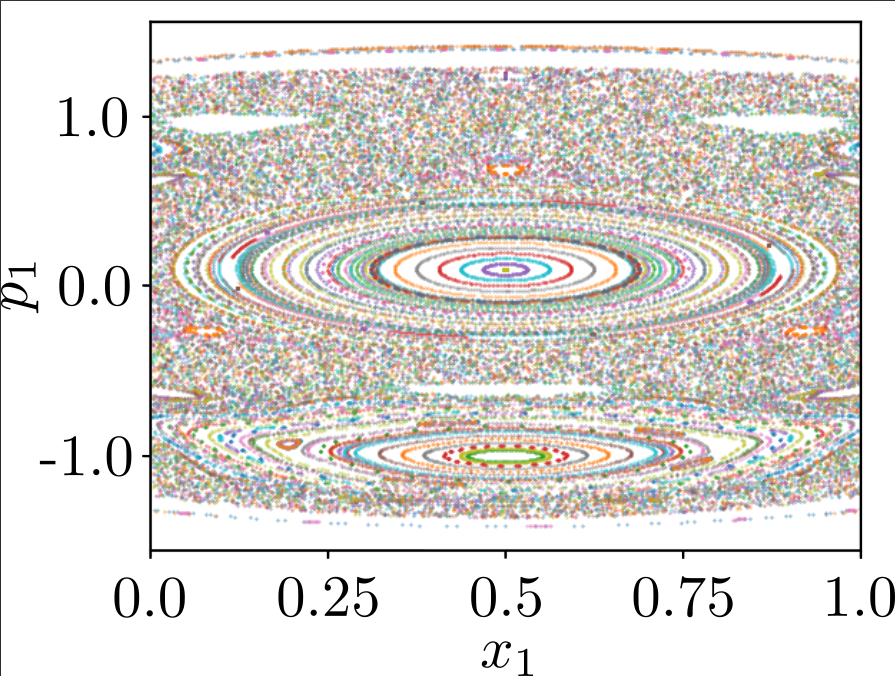
Poincare Surfaces of Section für zwei Teilchen. Diese ist eine Methode, um zu erkennen, wie chaotisch ein System ist. Chaotische Regionen sind punktiert, reguläre Bereich sind als ‘Ringe’ erkennbar. Erhöht man die Teilchenzahl, ist das ganze System chaotisch.

Wir haben auch Chaos für unser Modell gemessen. Wir haben herausgefunden, dass es vollkommen chaotisch wird, wenn man immer mehr Teilchen hinzufügt. Allerdings kann auch für sehr viele Teilchen Anfangsbedingungen finden, die gar nicht oder sehr langsam in ein Gleichgewicht gelangen. Dies wird allerdings immer schwieriger, so dass das in der Natur nicht vorkommt. Unsere Ergebnisse dazu haben wir auch in einer Publikation veröffentlicht [Hahn D. et al, Phys. Rev. E 103, 052213].

Die Mitgliedschaft im Forschungsstudiengang ermöglichte es mir, Kontakt zu Herrn Prof. Sondhi aufzubauen und hat mir den Aufenthalt an der Princeton University ermöglicht, auch in finanzieller Hinsicht. Diese drei Monate waren für mich ein unvergessliches Erlebnis. Ein besonderes Highlight war auch die Teilnahme am Empfang von James Peebles anlässlich der Bekanntgabe des Nobelpreises 2019.