Eigenstates of the Lewis-Riesenfeld invariant for de Sitter and quasi-de Sitter universes

Abstract

Motivated from considerations in theoretical cosmology about fluctuations in the very early universe, the aim of the project was to investigate the spectrum of the Lewis-Riesenfeld invariant, an invariant of the time-dependent harmonic oscillator Hamiltonian, and to analyse the behaviour of its two lowest eigenstates in position representation.

Scientific background

The nature of the very early universe right after the Big Bang and the processes that took place there are still opaque and content of research in modern cosmology. One rather new mechanism in this research direction is so-called inflation. It was introduced in the 1980s to solve a list of existing issues that had arisen before, like for instance the horizon problem, which states that even though there has never been any chance for all parts of the universe to be in causal contact with each other, one measures the same temperature of the cosmic background radiation from any direction. To cure this and further problems, a phase of exponential expansion of our universe lasting fractions of a second was proposed – known as inflation. The emergence of inflation might be for instance be caused by a scalar field $\phi$ , which is usually called inflaton. Starting from Einstein’s equations, that link the geometry of the universe to its matter content (and vice versa), one can derive an equation of motion for the inflaton field, using the cosmological principle, which says that on large scales the universe is homogeneous (looks the same everywhere) and isotropic (looks the same in every direction). These assumptions simplify Einstein’s equations and one obtains the so-called Friedmann equations, in which the dynamics of the universe reduces to one single scale factor $a(\eta)$ . Here, $\eta$ denotes the conformal time with values from $-\infty$ (Big Bang) to $0$ (today). If one then supposes that in this early universe matter was much less important than another contribution, called cosmological constant (which may correspond to dark energy today and to the inflaton field in the early universe), one ends up with a so-called de Sitter universe.

However, our everyday experience and measurements of the cosmic background radiation show that there are tiny fluctuations in the homogeneity and isotropy of the universe. In order to account for them, one can apply cosmological perturbation theory to the early universe, that is to consider perturbations of the geometric as well as the inflaton degrees of freedom and take a cosmological solution as the background. Due to the freedom of coordinate choice in General Relativity, one has to find observable quantities, that is physical quantities that are independent of specific coordinates. One of these so-called observables is the Mukhanov-Sasaki variable $v(\eta,\vec{x})$ which in a certain fixed coordinate system is given as $v(\eta,\vec{x}) = a(\eta) \; \delta\phi(\eta,\vec{x})$ , that is just the product of the scale factor of the universe times the linear perturbation of the inflaton field. It turns out that the equation of motion for this Mukhanov-Sasaki variable, called Mukhanov-Sasaki equation, can be written down in Fourier space as $\left( \frac{\partial^2}{\partial \eta^2} + \omega_{\vec{k}}^2(\eta) \right) v_{\vec{k}}(\eta)=0$ , with $v_{\vec{k}}(\eta)$ denoting the Fourier transform of $v(\eta,\vec{x})$ . For each $\vec{k}$ , this is just the equation of motion of a harmonic oscillator with time-dependent frequency $\omega_{\vec{k}}(\eta)$ . Some further evaluations then yield the frequency in a de Sitter universe to be $\omega_{\vec{k}}(\eta)=\vec{k}^2 - \frac{2}{\eta^2}$ . Since here the work is carried out in a perturbative framework, de Sitter is only the background solution, so also an evaluation of the considerations on a slightly modified universe that approximately is a de Sitter universe is interesting. Such a universe is called quasi-de Sitter and in that case the frequency in the Mukhanov-Sasaki equation is given as $\omega_{\vec{k}}(\eta)=\vec{k}^2 - \frac{1}{\eta^2} \left( \nu^2-\frac{1}{4}\right)$ with $\nu$ close to $\frac{3}{2}$ . Note that for $\nu = \frac{3}{2}$ one would again get the de Sitter result.

So far it turned out that the Mukhanov-Sasaki equation is appropriate to describe the evolution of the gauge invariant linear inflaton perturbation and that it has the form of an equation of motion of a harmonic oscillator with time-dependent frequency $\omega_{\vec{k}}(\eta)$ for every mode $\vec{k}$ . This result is of advantage because time-dependent harmonic oscillators have already been extensively studied in the physics literature . To analyse the equation further, the transition to the corresponding quantum theory is made and therefore the interest focuses on investigating the spectrum of a quantised version of the Hamiltonian of a time-dependent harmonic oscillator. This task can be simplified by introducing a quantity that is invariant under the time evolution generated by this time-dependent Hamiltonian. It is called the Lewis-Riesenfeld invariant $I_{LR}(\eta)$ and the corresponding quantised operator is given by $\hat{I}_{LR}(\eta) = \frac{1}{2} \left( (\xi(\eta) \hat{p} - \xi'(\eta)\hat{q})^2 + \frac{\omega_0^2 \hat{q}^2}{\xi^2(\eta)} \right)$ , where $\hat{q}$ and $\hat{p}$ are the position and momentum operator of the oscillator, $\omega_0$ a fixed frequency and $\xi(\eta)$ has to fulfill the so-called Ermakov equation to guarantee the invariance: $\left( \frac{d^2}{d\eta^2} +\omega^2(\eta) \right) \xi(\eta) - \omega_0^2 \xi(\eta)^{-3} = 0$ . As the Lewis-Riesenfeld invariant is an invariant of the time-dependent harmonic oscillator Hamiltonian, one can focus on determining its spectrum instead of the one of the latter.

Main research question and results

The main task of the project was to investigate the spectrum of the Lewis-Riesenfeld invariant on a quasi-de Sitter spacetime using the position representation and to analyse the behaviour of the lowest two eigenstates. The project was related to a shortly before completed Master’s thesis in the group (see citation [2] in the report below), where several tools which were needed in the project had been developed and where also the investigation of the de Sitter case had been carried out. One result of the Master’s thesis was the explicit derivation of a so-called Bogoliubov transformation $\hat{\Gamma}_{\xi}$ that maps the eigenstates of a time-independent harmonic oscillator $| n \rangle$ to the ones of the Lewis-Riesenfeld invariant $| \lambda_n, \eta \rangle$ , where $\hat{I}_{LR} |\lambda_n \rangle = \lambda_n |\lambda_n, \eta\rangle$ , by $\hat{\Gamma}_{\xi}^\dagger | n \rangle = | \lambda_n, \eta \rangle$ .
It also transforms the ladder operators of the time-independent harmonic oscillator $\hat{a}^{(\dagger)}$ into the ones corresponding to the Lewis-Riesenfeld invariant, $\hat{a}^{(\dagger)}(\eta)$ by $\hat{\Gamma}_{\xi}^\dagger \hat{a}^{(\dagger)} \hat{\Gamma}_{\xi} = \hat{a}^{(\dagger)}(\eta)$ . The special features of a Bogoliubov transformation are that it is unitary and that the commutators of the ladder operators remain invariant under this transformation, that is $[\hat{a},\hat{a}^\dagger ] = [\hat{a}(\eta), \hat{a}^\dagger(\eta)]=1$ . In the Master’s thesis there had also been computed explicit expressions for the ladder operators and the Bogoliubov transformation in terms of position and momentum operators and $\xi$ .

General expression for the spectrum of the Lewis-Riesenfeld invariant in position representation

Starting from the condition that the lowering operator applied to the vacuum should give zero, $\hat{a} | 0 \rangle = 0$ , one can perform a Bogoliubov transformation of this equation to end up with $\hat{a}(\eta) |\lambda_0,\eta\rangle =0$ . Evaluating this in position representation gives a differential equation for the ground state $\psi_0(q,\eta) := \langle q | \lambda_0,\eta \rangle$ . Solving this equation and requiring proper normalisation, one obtains an expression for $\psi_0(q,\eta)$ which depends on $\xi$ . Acting on the result with the raising operator in position representation then yields the first excited state in terms of $q, \eta$ and $\xi$ . Iteration of this procedure gives the entire spectrum of the Lewis-Riesenfeld invariant, $\psi_n(q,\eta) = \langle q | \lambda_n,\eta \rangle = \langle q | \frac{1}{\sqrt{n!}} \left(\hat{a}^\dagger_\xi \right)^n | \lambda_0,\eta \rangle$ .

Solution of the Ermakov equation on quasi-de Sitter

So far, the spectrum still depends on the variable $\xi(\eta)$ which encodes the dynamics of the spacetime under consideration. In the Master’s thesis there was outlined a way to construct this property for a general spacetime based on two linearly independent solutions of the classical Mukhanov-Sasaki equation, where the chosen $\omega_{\vec{k}}(\eta)$ determines the spacetime under consideration. As mentioned above, for the quasi-de Sitter case this is $\omega_{\vec{k}}(\eta)=\vec{k}^2 - \frac{1}{\eta^2} \left( \nu^2-\frac{1}{4}\right)$ . After introduction of new variables and a rescaling, the Mukhanov-Sasaki equation can be recast into the form of a generalised Bessel differential equation with parameter $\nu$ . Two linearly independent solutions are then given either by using Bessel and Neumann functions, or in terms of Hankel functions. In the project it turned out to be fruitful to use both sets of solutions. With them, it was possible to derive the form of $\xi(\eta)$ . This involved several steps, among others to calculate the Wronskian determinant of the Bessel functions of the different kinds. The asymptotic behaviour of the latter was used to get normalised and well-defined results and helped to determine unknown coefficients in the expression for $\xi(\eta)$ . As a consistency check, it turned out that for the special choice $\nu = \frac{3}{2}$ the result was equal to the one obtained for the de Sitter case, as expected.

The lowest two states of the spectrum

Using this solution for $\xi(\eta)$ in the lowest wave functions $\psi_0(q,\eta)$ and $\psi_1(q,\eta)$ , one finds the form of these states in position representation and can plot the probabilities $|\psi_n(q,\eta)|^2$ for different values of $\nu$ . The last step of the project then consisted in a qualitative analysis of how the ground and first excited state look like in general and which difference arises if one goes from de Sitter ( $\nu = \frac{3}{2}$ ) to quasi-de Sitter, for which exemplarily $\nu = 1.45$ and $\nu = 1.55$ were chosen. It turned out that the ground state possesses a maximum at the origin, while the first excited state has a minimum there and two maxima at positions $q=\pm b_{\nu}$ . The parameter $\nu$ determines the position of the maxima $b_{\nu}$ and also affects the width of the probability distribution at fixed times. Regarding different times, the states remain almost constant, just for times close to $\eta=0$ they diffuse and spread. Below there can be seen a sample plot of ground and first excited state for the three choices of $\nu$ mentioned above at two fixed times.

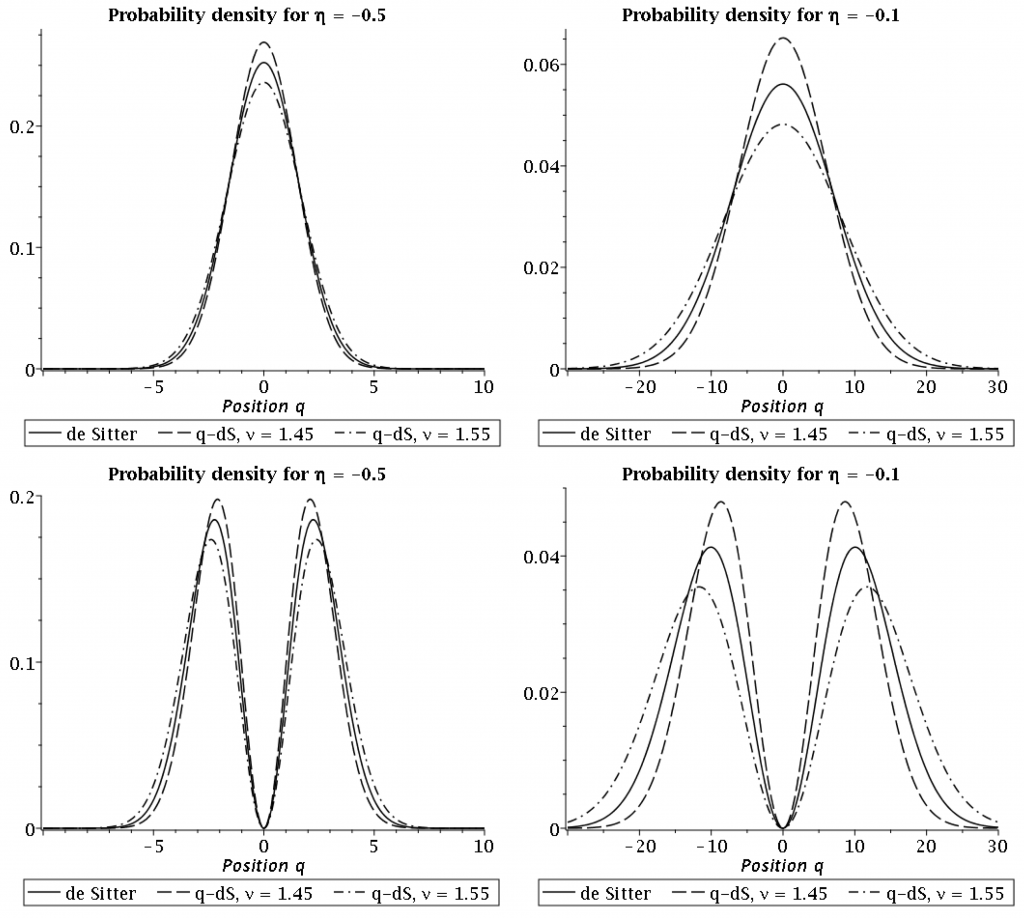
Plots
(Plot was also published in the paper cited below.)

Requirements

Prerequisite for the project was a good knowledge of quantum mechanics. No prior knowledge in cosmology or General Relativity was necessary, the required basics were introduced during the project.